1. Introduction:
   1. How to Write the Equations:
   2. Filter Schematic:
   3. Filter Node Schematic:
   4. Filter Node Equations:
   5. Filter Spec's (Component values and frequency sweep range)
   6. Filter Program Test Results:

I got interested in the Python computer language and started making multi-dimensional lists (matrix). This lead me to wonder what application I could write using Python. I decided to try and solve a set of linear equations using Matrix Algebra. I designed a Python program for analyzing both DC and AC circuits using Mash and Node analysis. All went will until I wanted to analyze an Active Circuit implemented with Operational Amplifiers (Op-Amps).  I searched the Web looking for information on writing Node Equations for Active Circuits. I did find some papers written by several professors saying that superposition could be used when current and voltage generators in a given node/mash where a functions of another node/mash. These professors also noted that many electronics book authors have stated that superposition could not be used in this situation. So, with this information, I decided to figure out how to apply my program to anlalyze an active filter I invented many years ago called the "Bainter Filter" by some people on the Internet. See article published in the October 2, 1975 issue of Electronics magazine.

 

An Op-Amp  Fig. 1  


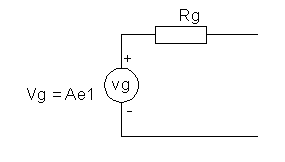
Op-Amp Thevenin equivalent voltage generator  Fig. 2


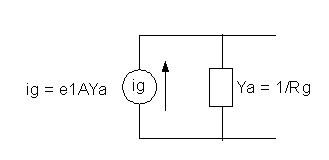
Op-Amp Norton equivalent current generator  Fig. 3

All Op-Amps need to be converted to their Norton equivalent current generators as per Fig. 3 where e1 is the node voltage driving the Op-Amp, A is the open loop gain, and Ya is the output admittance of the amplifier.

Filter Schematic:

This filter contains three op-amps. Op-Amp K1 in an inverter (gain = -1.0). Op-Amp K2 is a unity gain buffer (gain = +1.0). The center Op-Amp is the one of interest. It has an open loop gain of -A as it is connected as an inverting amplifier.

We will next convert each Op-Amp to it's Norton current generator in order to write the node analysis equations.

Filter Node Schematic:

NOTE: All current generators point into their respective nodes. The sign of the Op-Amp connection is determined by the value of the symbols K1, A, and K2. For this filter K1 = -1.0, A (open loop gain) = - 100,000, and K2 = 1.0. Op-Amps K1 and A are inverting and K2 is non-inverting.

Filter Node Equations:

NOTE: Each value of  capacitance must be multiplied by "s" where s = j*2*PI*f where "j" is used in Python to indicate a complex number and "f" is the frequency. The s's have been left out in order to simplify the equations below  because the program I wrote did this operation for each frequency as the program runs.



The voltage E4 at node 4 is a function of the voltage E3 at node 3; therefore the entry of -ya*A-c1 in cell 4-E3 in the above matrix. In this example, the amplifer gain has been defined as a negitive number. The mutual node four has a negative value because it is connected to the inverting (negative) input of the amplifer. If there would have been a mutual node for the positive input of the amplifer, it's repective equation would have a positive sign. If the gain is defined with a positive value the mutual node equations will have signs opposite from this example.

Gain sign negative: mutual equation sign same as amplifer input sign.
Gain sign positive: mutual equation sign opposite of amplifer input sign.

Filter Spec's (Component values and frequency sweep range)

Filter Program Test Results:

Following is a graph of the filter tuned to 1000 Hz. The plot was made by the Python program I wrote using the equations in this document.

---

Last updated:  6 June 2012        Contact:  Jim Bainter